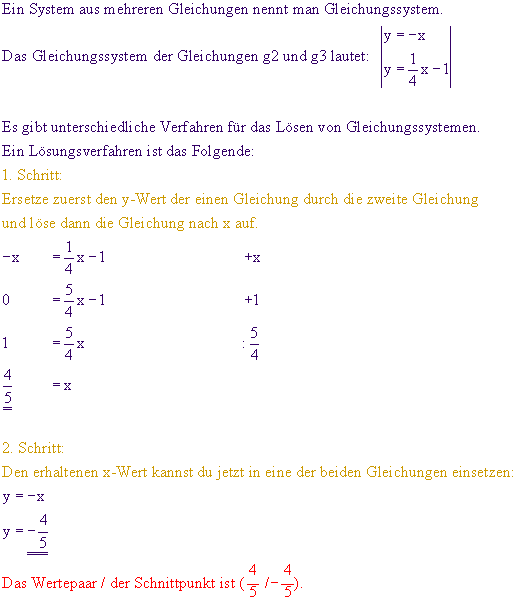Lineare Funktion: Geradengleichung und Gleichungssystem

Tipp 1

Merke dir die Begriffe "Negative Steigung", "Positive Steigung" und "Ursprungsgerade".

Negative Steigung:
Du startest bei einem Punkt der Geraden, machst einen Schritt der Länge 1 nach rechts und musst dann nach unten steigen bis du wieder zu einem Punkt der Geraden kommst.
Positive Steigung:
Du startest bei einem Punkt der Geraden, machst einen Schritt der Länge 1 nach rechts und musst dann nach oben steigen bis du wieder zu einem Punkt der Geraden kommst.

Die Geraden g1 und g2 haben eine negative Steigung, die Gerade g3 hat eine positive Steigung.

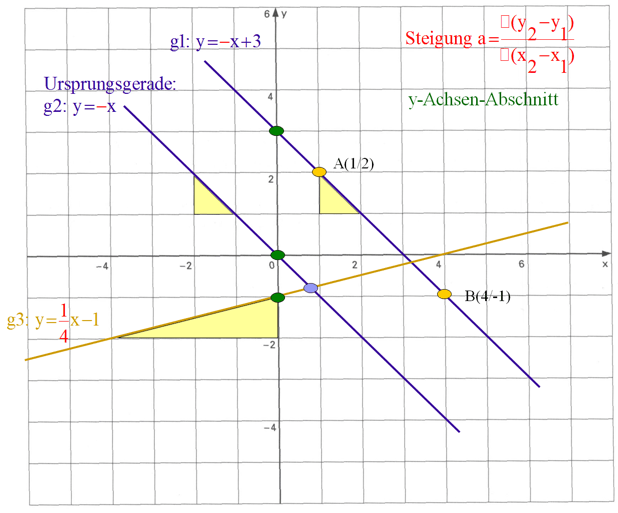
Ursprungsgerade:
Eine Ursprungsgerade verläuft durch den Koordinatenpunkt (0/0) (= Ursprung). Die Gerade g2 ist eine Ursprungsgerade.

Tipp 2

Wenn du die Steigung nicht aus der Grafik ablesen kannst, dann gehe folgendermassen vor:

Hinweis 3

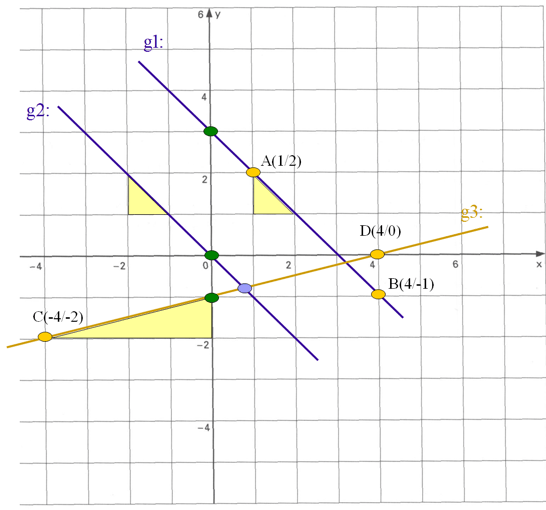
Und wie erhältst du die Funktionsgleichung der Geraden g3? Du benötigst zur Steigung a auch den y-Achsen-Abschnitt b. Du erhältst den y-Achsenabschnitt indem du einen beliebigen Punkt der Geraden in die Geradengleichung (von der du ja schon die Steigung kennst) einsetzt.

Hinweis 4

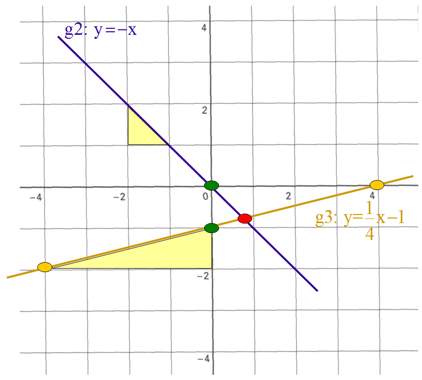
Wie findest du den Schnittpunkt zweier Geraden? Schau dir den Schnittpunkt der Geraden g2 und g3 unten in der Grafik an. Das Wertepaar (x/y) des Schnittpunktes, ist sowohl Lösung der Gleichung g2 als auch der Gleichung g3.