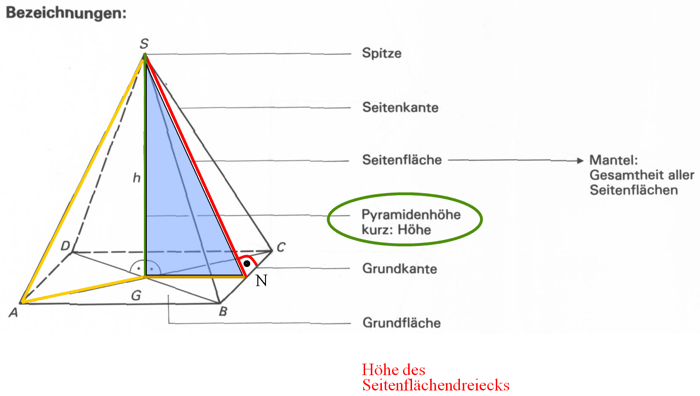
Pyramiden

Tipp 1

Prüfe, ob du die folgenden Begriffe kennst: Grundfläche, Seitenfläche, Grundkante, Seitenkante, Pyramidenhöhe, Höhe des Seitenflächendreiecks

Hinweis 2

Oft musst du mit Hilfe des Satzes von Pythagoras Höhen und Kanten berechnen. Den Satz des Pythagoras kannst du deshalb anwenden, weil du es mit rechtwinkligen Dreiecken zu tun hast. Betrachte in der Grafik oben das blaue Dreieck GNS. Wenn du beispielsweise die Hälfte der Grundkante (GN) und die Pyramidenhöhe h kennst, dann kannst du die Höhe des Seitenflächendreiecks berechnen.

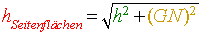
Hinweis 3

Auch das gelbe Dreieck AGS ist rechtwinklig. Betrachte es zuerst in der Grafik oben (Tipp 1) und dann hier. Du hast jetzt das Netz der Pyramide vor dir. Du erkennst nun, dass es sich um eine quadratische Pyramide handelt.

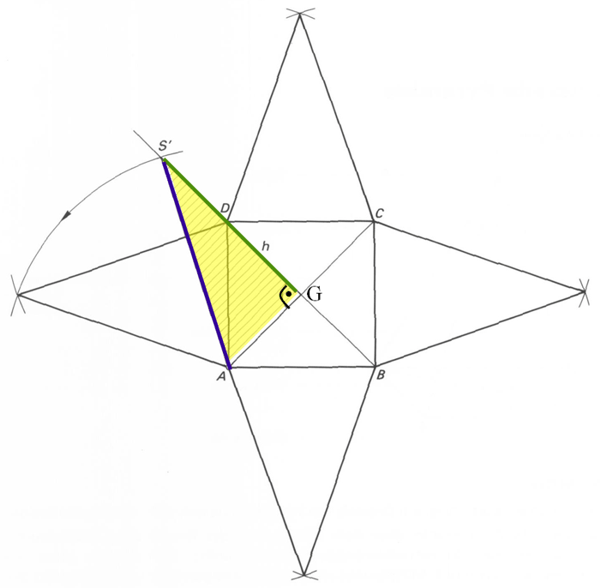
Die Diagonale kannst du aus den Grundkanten berechnen. Die Seitenkante k erhältst du wiederum mit Hilfe des Satzes von Pythagoras:

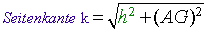
Tipp 4

Merke dir, welche Grössen für die Berechnung des Volumens einer Pyramide nötig sind.

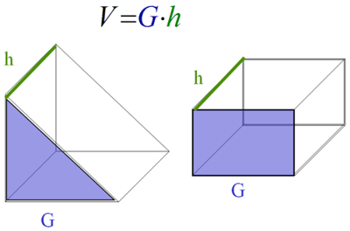
Von Bedeutung sind nur Grundfläche und Höhe. Du erinnerst dich sicher an die Volumenberechnung von Quadern und Prismen. Die Formel lautete Grundfläche mal Höhe. Auch dort waren also Grundfläche und Höhe die entscheidenden Grössen:

Neu ist jetzt bei der Berechnung von Pyramidenvolumen der Faktor 1/3.
Das Volumen von Pyramiden ist ein Drittel eines Prismas mit gleicher Grundfläche und gleicher Höhe!

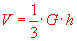
Es ist unbedeutend welche Form die Grundfläche der Pyramide besitzt.